|
|
Derivatives
[Printer Friendly Version]
| d |
 |
| dx |
| [k] = 0 |
|
| d |
 |
| dx |
| [x] = 1 |
|
| d |
 |
| dx |
| [kx] = k |
|
| d |
 |
| dx |
| [xn] = n · xn – 1 | (1) |
|
|
| d |
 |
| dx |
| [kxn] = n · kxn – 1 | (1) | |
| d |
 |
| dx |
| [k · u] = k · u’ |
|
| d |
 |
| dx |
| [u + v] = u’ + v’ | (2) |
|
| d |
 |
| dx |
| [u – v] = u’ – v’ | (3) |
|
|
| d |
 |
| dx |
| [uv] = vu’ + uv’ | (4) |
|
| d | 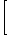 |
 |
| dx |
|
| u |
 |
| v |
|
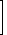 | = |
| vu’ – uv’ |
 |
| v² | | (5) |
|
| d |
 |
| dx |
| [f(u)] = f ’(u) · u’ | (6) |
|
|
- Difference Rule
- Product rule
|
|
|
|
|
| d |
 |
| dx |
| [ex] = ex |
|
| d |
 |
| dx |
| [eu] = eu · u’ |
|
| d |
 |
| dx |
| [ax] = ln(a) · ax |
|
|
| d |
 |
| dx |
| [loga(x)] = |
| 1 |
 |
| ln(a) · x |
|
|
| d |
 |
| dx |
| [ln(x)] = |
| 1 |  |
| x |
|
|
| d |
 |
| dx |
| [ln(u)] = |
| 'u’ |
 |
| 'u’ |
|
|
|
| d |
 |
| dx |
| [sin(x)] = cos(x) |
|
| d |
 |
| dx |
| [cos(x)] = –sin(x) |
|
| d |
 |
| dx |
| [tan(x)] = sec²(x) = |
| 1 |  |
| cos²(x) |
|
|
|
| d |
 |
| dx |
| [csc(x)] = –csc(x) · cot(x) |
|
| d |
 |
| dx |
| [sec(x)] = sec(x) · tan(x) |
|
| d |
 |
| dx |
| [cot(x)] = –csc²(x) |
|
|
| d |
 |
| dx |
| [arcsin(x)] = |
| 1 |  |
| √(1 – x²) |
|
|
| d |
 |
| dx |
| [arccos(x)] = |
| –1 |  |
| √(1 – x²) |
|
|
| d |
 |
| dx |
| [arctan(x)] = |
| 1 |  |
| 1 + x² |
|
|
|
|
Today is
.
Web page designed and maintained by Wade A. Tisthammer
Last modefied: December 5, 2002
normandaleptk@hotmail.com
Phone number: (952) 487-8128
This web page was originally created by Wade A. Tisthammer. If you have any questions, comments, etc. you can e-mail him at tisthammerw@hotmail.com. This portion of text is meant to be used as a way for this web page to have the format that it does.
|
|
|

